Home
README

Advanced Volatility and Risk-Adjusted Return Indicator

Educational Tool for Traders & Indie Language Learners `v1.0 | For educational use | All experience levels`

What This Indicator Does

This tool combines three foundational financial concepts into a single visualization, bridging technical analysis with portfolio theory:

Metric	Formula/Core Concept	What It Reveals
Standard Deviation (Yellow)	`σ = √[Σ(x - μ)² / N]`	Price volatility risk over time
Sharpe Ratio (Blue)	`(Return - Risk-Free Rate) / σ`	Quality of risk-adjusted returns
ARCH Volatility (Red)	Nobel-winning volatility clustering model	Market turbulence regimes

Why It Matters for Traders

Risk Awareness:
- Rising StdDev → Expanding risk (prepare for larger swings)
- High Sharpe → Efficient capital allocation (validate strategy edges)
- ARCH spikes → Early warning for volatility regimes (hedging signals)
Cross-Market Insights:
- Works on stocks, crypto, forex (adjust vol_scale per asset)
- Compare assets: Higher Sharpe = better risk/reward profile
Educational Value:
- Visualizes Robert Engle’s Nobel-winning ARCH model in action
- Demonstrates modern portfolio theory (MPT) fundamentals

Code Logic for Developers

Key Indie Language Features Demonstrated:

# 1. Parameterization with decorators
@param.int('stddev_length', default=20)
@param.float('risk_free_rate', default=0.01)
# 2. Series handling & mutable data
returns = MutSeriesF.new(0)
returns[0] = (self.close[0] - self.close[1]) / self.close[1]
# 3. Built-in algorithms
stddev = StdDev.new(returns, stddev_length)[0]
# 4. Annualization logic (real-world scaling)
daily_rf = (1 + risk_free_rate) ** (1/252) - 1
sharpe_ratio = (annual_return - risk_free_rate) / annual_volatility

Best Practices Illustrated:

Parameter validation (min=1 guards)
Safe division checks (if ... != 0)
Volatility scaling for visual clarity

Learning Pathways

For Traders:

Study ARCH spikes during FOMC/news events
Backtest strategies when Sharpe > 1.5
Compare StdDev vs. ARCH to detect “quiet before storm” patterns

For Indie Developers:

Learn series mutation with MutSeriesF
Practice timeframe conversions (daily→annual)
Explore decorator-based parameter systems

Visualization Tips

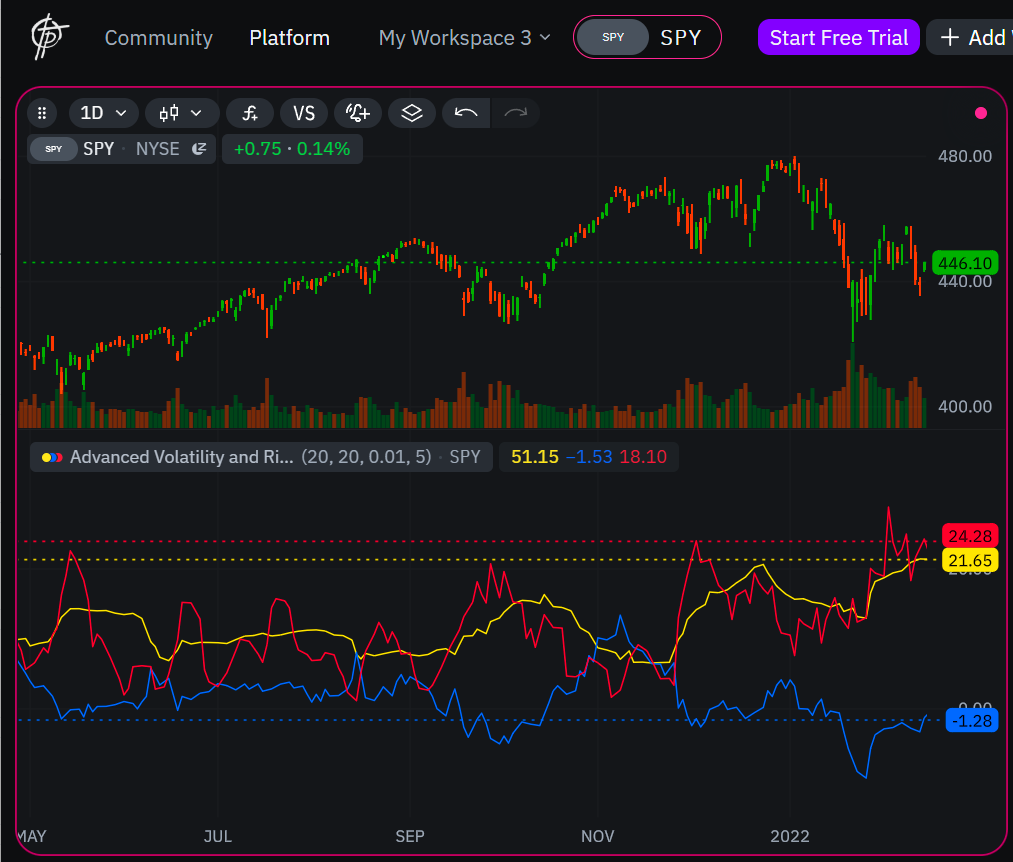Indicator Preview Color coding: Yellow=StdDev, Blue=Sharpe, Red=ARCH

Crypto (1D): Use vol_scale=100, watch ARCH during BTC halvings
Stocks (1H): Set risk_free_rate=0.03 (T-bill rate), track sector rotations
Forex (15M): arch_lag=3 for intraday volatility clusters

Theoretical Foundation

Modern Portfolio Theory (MPT): Sharpe Ratio optimization
Volatility Clustering: Engle’s ARCH model (Nobel 2003)
Risk-Adjusted Returns: Excess Return / Unit Risk framework*“This isn’t just an indicator—it’s a window into how quants model markets.”*

Indie v5 Script code

#education purpose
# indie:lang_version = 5
import math
from indie import indicator, param, plot, color, MutSeriesF
from indie.algorithms import StdDev, Sma

@indicator('Advanced Volatility and Risk-Adjusted Return Indicator', overlay_main_pane=False)
@param.int('stddev_length', default=20, min=1, title='Standard Deviation Length')
@param.int('sharpe_length', default=20, min=1, title='Return Period for Sharpe Ratio')
@param.float('risk_free_rate', default=0.01, title='Risk-Free Rate (annual)')
@param.int('arch_lag', default=5, min=1, title='ARCH Lag')
@param.float('vol_scale', default=100.0, min=1.0, title='Volatility Scaling Factor')
@plot.line(color=color.YELLOW, title='Standard Deviation')
@plot.line(color=color.BLUE, title='Sharpe Ratio')
@plot.line(color=color.RED, title='ARCH Volatility')
def Main(self, stddev_length, sharpe_length, risk_free_rate, arch_lag, vol_scale):
    # 1. Calculation of daily returns
    returns = MutSeriesF.new(0)
    if len(self.close) > 1 and self.close[1] != 0:
        returns[0] = (self.close[0] - self.close[1]) / self.close[1]
    
    # 2. Annual risk-free rate → daily
    daily_rf = (1 + risk_free_rate) ** (1/252) - 1
    
    # 3. Volatility (standard deviation)
    stddev_daily = StdDev.new(returns, stddev_length)[0]
    stddev_annual = stddev_daily * math.sqrt(252) * vol_scale
    
    # 4. Sharpe Ratio
    avg_return_daily = Sma.new(returns, sharpe_length)[0]
    avg_return_annual = avg_return_daily * 252
    sharpe_ratio = (avg_return_annual - risk_free_rate) / (stddev_annual / vol_scale) if (stddev_annual / vol_scale) != 0 else 0
    
    # 5. ARCH volatility
    mean_return = Sma.new(returns, arch_lag)[0]
    squared_dev = (returns[0] - mean_return) ** 2
    arch_vol_daily = math.sqrt(Sma.new(MutSeriesF.new(squared_dev), arch_lag)[0])
    arch_vol_annual = arch_vol_daily * math.sqrt(252) * vol_scale
    
    return stddev_annual, sharpe_ratio, arch_vol_annual

Pine Script 5 code

//@version=5
indicator("Advanced Volatility and Risk-Adjusted Return Indicator", overlay=false)

// Input parameters
stddev_length = input.int(20, title="Standard Deviation Length", minval=1)
sharpe_length = input.int(20, title="Return Period for Sharpe Ratio", minval=1)
risk_free_rate = input.float(0.01, title="Risk-Free Rate (annual)")
arch_lag = input.int(5, title="ARCH Lag", minval=1)
vol_scale = input.float(100.0, title="Volatility Scaling Factor", minval=1.0)

// 1. Daily returns
returns = nz(close / close[1] - 1)

// 2. Convert annual risk-free rate to daily
daily_rf = math.pow(1 + risk_free_rate, 1 / 252) - 1

// 3. Volatility (standard deviation)
stddev_daily = ta.stdev(returns, stddev_length)
stddev_annual = stddev_daily * math.sqrt(252) * vol_scale

// 4. Sharpe Ratio
avg_return_daily = ta.sma(returns, sharpe_length)
avg_return_annual = avg_return_daily * 252
sharpe_ratio = (avg_return_annual - risk_free_rate) / (stddev_annual / vol_scale)
sharpe_ratio := na(stddev_annual / vol_scale) or (stddev_annual / vol_scale == 0) ? 0 : sharpe_ratio

// 5. ARCH Volatility
mean_return = ta.sma(returns, arch_lag)
squared_dev = math.pow(returns - mean_return, 2)
arch_vol_daily = math.sqrt(ta.sma(squared_dev, arch_lag))
arch_vol_annual = arch_vol_daily * math.sqrt(252) * vol_scale

// Plotting
plot(stddev_annual, color=color.yellow, title="Standard Deviation")
plot(sharpe_ratio, color=color.blue, title="Sharpe Ratio")
plot(arch_vol_annual, color=color.red, title="ARCH Volatility")

Sources: repo

License: CC BY-NC 4.0 (Educational use) Documentation: Indie Language Wiki Contributions: Open-source @ *Created for the TakeProfit.com Community by Pavel Medd

Advanced Volatility and Risk-Adjusted Return Indicator

Table of Contents